ต่อกันด้วยหัวข้อสุดท้ายจากเนื้อหาบทภาคตัดกรวย คณิตศาสตร์ ม.4 นะครับ กับสมการไฮเพอร์โบลา ที่รูปร่างหน้าตาจะคล้ายๆกับสมการพาราโบลาที่กำลังส่องกระจกอยู่ เจ้าไฮเพอร์โบลาจะมีสูตรสมการที่ซับซ้อนขึ้นเล็กน้อย แต่จะมีสูตรในการจำและแยกแยะซึ่งถ้าดูเป็นแล้ว แยกง่ายมาก แค่เครื่องหมาย ± เองครับ
หลายคนอาจจะยังไม่รู้จักว่าไฮเพอร์โบลาคืออะไร เรามาลองทำความรู้จักกันมันดูกันนะครับ สมการไฮเพอร์โบลาในปัจจุบันได้ถูกตั้งชื่อโดยนักคณิตศาสตร์ชาวกรีกที่ชื่อว่า Apollonius ต่อมานักคณิตศาสตร์ชื่อ Pappus ได้ค้นพบจุดที่เรียกว่าจุดโฟกัส (Focus) และเส้นไดเรกตริกซ์ (Directrix) โดยสมการไฮเพอร์โบลานี้มีรูปร่างมาจากวงโคจรของดาวบริวารรอบดวงอาทิตย์
นิยามของสมการไฮเพอร์โบลา
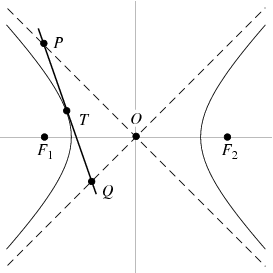
ไฮเพอร์โบลา (Hyperbola) คือเซตของจุดทั้งหมดในระนาบซึ่งผลต่างของระยะทางจากจุดใดๆไปยังจุด F1 และ F2 ที่ตรึงอยู่กับที่มีค่าคงตัว โดยค่าคงตัวน้อยกว่าระยะห่างระหว่างจุดคงที่ที่ตรึงอยู่กับที่ทั้งสอง จุด F1 และ F2 ดังกล่าวนี้เรียกว่า โฟกัส (Focus) ของไฮเพอร์โบลา
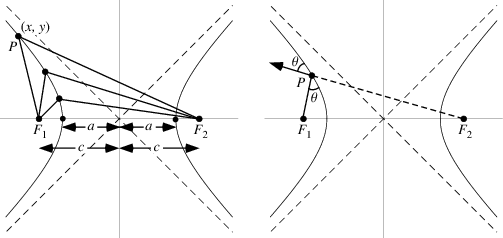 ให้ระยะทางจากจุด F1 และ F2 ไปยังเส้นกราฟมีค่าเท่ากับ r1=F1 และ r2=F2 และระยะทางระหว่างจุด F และจุด F2 มีค่าเท่ากับ 2c หรือเรียกอีกอย่างว่าค่า k ซึ่งค่า k นี้จะมีค่าเป็นบวกเสมอ
ให้ระยะทางจากจุด F1 และ F2 ไปยังเส้นกราฟมีค่าเท่ากับ r1=F1 และ r2=F2 และระยะทางระหว่างจุด F และจุด F2 มีค่าเท่ากับ 2c หรือเรียกอีกอย่างว่าค่า k ซึ่งค่า k นี้จะมีค่าเป็นบวกเสมอ
r2-r1 = k
ถ้าจุด P ซึ่งอยู่บนเส้นกราฟด้านซ้ายมืออยู่บนแกน x แล้ว
k = (c+a) – (c-a) = 2a
ดังนั้นเราสามารถคำนวณค่า k=2a ได้ หรือนั่นก็คือระยะทางระหว่างจุดยอดของกราฟไฮเพอร์โบลาทั้งสอง ข้อสังเกตุคือเส้นกราฟพาราโบลาที่เกิดจาดจุดโฟกัส F1 จะมีเส้นกราฟที่เกิดจาด F2 สะท้อนเหมือนกันอยู่ในฝั่งตรงข้ามเสมอ
สมการไฮเพอร์โบลา
รูปแบบของสมการไฮเพอร์โบลาจะแบ่งออกตามรูปกราฟสมการสองแบบ คือไฮเพอร์โบลาแบบตะแคง (ซ้ายขวา) และไฮเพอร์โบลาแบบตั้ง (บนล่าง) โดยทั้งสองรูปแบบมีสมการดังนี้
| ไฮเพอร์โบลาตะแคง | ไฮเพอร์โบลาตั้ง |
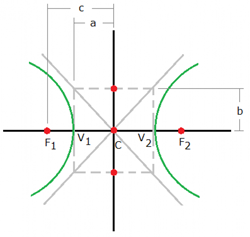 สมการไฮเพอร์โบลาคือ สมการไฮเพอร์โบลาคือ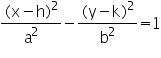 ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้ ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้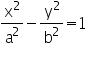 สังเกตว่าหน้า x เป็นบวก ดังนั้นแกนตามขวางจึงวางตัวในแนวแกน x (a อยู่กับ x)แกนตามขวาง (แกนที่ลากตัดกึ่งกลางของกราฟ) มีความยาวเป็น 2a แกนสังยุค มีความยาวเป็น 2b ระยะโฟกัส มีความยาว
| 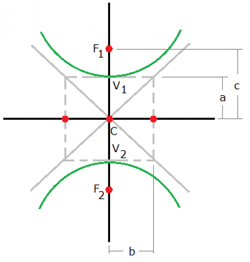 สมการไฮเพอร์โบลาคือ สมการไฮเพอร์โบลาคือ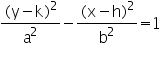 ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้ ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้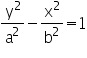 สังเกตว่าหน้า x เป็นบวก ดังนั้นแกนตามขวางจึงวางตัวในแนวแกน x (a อยู่กับ x)แกนตามขวาง (แกนที่ลากตัดกึ่งกลางของกราฟ) มีความยาวเป็น 2a แกนสังยุค มีความยาวเป็น 2b ระยะโฟกัส มีความยาว |
ข้อสังเกตุ: a ไม่จำเป็นต้องยาวกว่า b เหมือนในสมการวงรี แต่ถ้า a=b จะได้สี่เหลี่ยมจัตุรัสอยู่ตรงกลาง จะเรียกว่าเป็น ไฮเพอร์โบลามุมฉาก (Rectangular Hyperbola)
โจทย์ไฮเพอร์โบลา
ตัวอย่างที่1: จงหาจุดศูนย์กลาง จุดโฟกัส จุดยอด ความยาวของแกนตามขวาง ความยาวแกนสังยุค ความยาวเส้นลาตัสเรกตัม ค่าเอ็คเซนตริกซิตี (e) และสมการเส้นกำกับของไฮเพอร์โบลาต่อไปนี้ พร้อมทั้งวาดกราฟ
![]()
วิธีทำ
ตัวเลขส่วนของสมการไฉเพอร์โบลาที่โจทย์ให้มาเป็นกำลังหนึ่ง แต่เราต้องการกำลังสองเพื่อเข้าสูตรไฮเพอร์โบลา จึงแปลงสมการนี้ให้อยู่ในรูปกำลังสองได้ดังนี้
![]()
ซึ่งเมื่อนำไปเทียบกับสมการมาตรฐานของไฮเพอร์โบลา
![]()
เราจะได้ค่า a=4, b=3
ใช้สูตรพีธากอรัสเพื่อหาค่า c ได้ดังนี้
c2 = a2 + b2
c2 = 42 + 32
c2 = 25
c = 5
เมื่อเราได้ค่า a, b, และ c มาครบแล้ว จะสามารถเขียนรูปกราฟได้ดังนี้
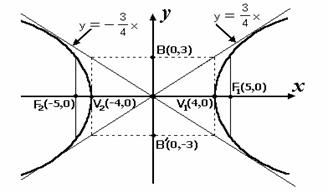
จากรูปและสมบัติของไฮเพอร์โบลา จะได้
จุดศูนย์กลางคือ (0,0)
จุดโฟกัส คือ (±5,0)
จุดยอด คือ (±4,0)
ความยาวของแกนตามขวาง 2a = 8
ความยาวแกนสังยุค 2b = 3
ความยาวเส้นเลตัสเรกตัม ![]()
สมการเส้นกำกับ ![]()
ค่าเอ็คเซนตริกซิตี (e) = c/a = 5/4 = 1.25
#Answer
ข้ามไปยังเนื้อหา:
สำหรับ คนที่สนใจอยากเรียนคณิตศาสตร์เรื่องภาคตัดกรวย และบทอื่นๆ แต่ไม่อยากอ่านเอง อยากดูในรูปแบบคลิปวีดีโอมากกว่า พี่มีของดีมาแนะนำครับ คลิปวีดีโอสอนเรื่องภาคตัดกรวยครบทุกหัวข้อ และบทเรียนอื่นๆในระดับชั้นมัธยมอีกครบถ้วน สอนอย่างละเอียดตั้งแต่เริ่มต้น พร้อมด้วยโจทย์เรื่องภาคตัดกรวยเรียงจากง่ายไปยาก ลองอ่านข้อความด้านล่างนี้ดูนะครับ


![[รีวิว] เรียนพิเศษออนไลน์ วิชาคณิตกับ dektalent.com - Tewfree](https://www.tewfree.com/wp-content/uploads/2020/02/website-400x209.png)

![รวมข้อสอบ O-NET ม.6 พร้อมเฉลย [Download] - Tewfree](https://www.tewfree.com/wp-content/uploads/2020/01/download-ข้อสอบ-o-net-400x209.jpg)







อธิบายพอเข้าใจนิดหน่อยครับ แถมได้โจทย์ไปแก้ข้อสอบ 1 ข้อด้วยครับ มีประโยชน์หน่อยๆครับ อุอุอิอิชิมะเค๊อะ!
??
ยากเกิ้น
2b = 6 ในเว็บเขียนผิดครับ
“สังเกตว่าหน้า x เป็นบวก ดังนั้นแกนตามขวางจึงวางตัวในแนวแกน x” ประโยคนี้ในไฮเปอร์โบล่าตั้งผิดครับ เพราะหน้า X เป็นลบ
แกนตามขวางต้องเป็นแกน Y