พาราโบลา (Parabola) คณิตศาสตร์ ม.4

มาถึงตอนที่สามของซีรียส์เรียนคณิตศาสตร์กับนายติวฟรีในบทเรียนภาคตัดกรวย มาถึงตอนที่ตอนนี้เป็นเรื่องของสมการพาราโบลา (Parabola) คณิตศาสตร์ ม.4 กันแล้วนะครับ สมการพาราโบลาเป็นเรื่องที่อาจจะเข้าใจยากในตอนแรกแต่ถ้ารู้เรื่องแล้วถือว่าเรียนสนุกครับ ลองมาเรียนกันนะ

นิยามของสมการพาราโบลา

พาราโบลา คือเซตของจุดบนพื้นระนาบซึ่งมีระยะห่างจากจุดคงที่ เท่ากับระยะที่ห่างจากเส้นคงที่

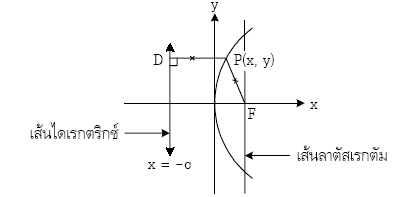
จุดคงที่ คือจุดโฟกัส (Focus)

เส้นตรงที่คงที่ คือเส้นไดเรกตริกซ์ (Directrix)

เส้นลาตัสเลกตัม (Latus Rectum) คือเส้นตรงที่ลากผ่านจุดโฟกัสและตั้งฉากกับแกนของรูป

แกนของรูปหรือแกนสมมาตร คือเส้นตรงที่ลากผ่านจุดยอดและผ่านจุดโฟกัส

คอร์ดของพาราโบลา คือเส้นตรงที่ลากเชื่อมจุด 2 จุด ที่ต่างกันของพาราโบลาและคอร์ดที่ลากผ่านจุดโฟกัสเรียกว่า Focul ส่วนคอร์ดที่ลากผ่านจุดโฟกัสด้วย และตั้งฉากกับแกนของรูปด้วย เรียกว่า ลาตัสเรกตัม (Latus Recrum)

ข้อสังเกตุ

จากสมการ จะต้องมีตัวแปรใดตัวแปรหนึ่งอยู่ในรูปกำลังสอง และอีกตัวหนึ่งยกกำลังหนึ่ง และอยู่ที่เทอมที่บวกลบกัน กราฟที่ได้จึงจะเป็นกราฟพาราโบลา

รูปแบบของพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (0,0)

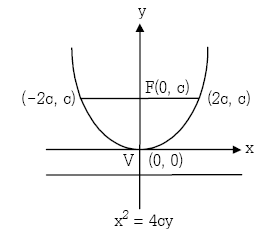พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน y

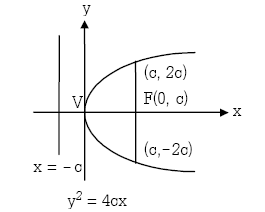พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน x

เราสามารถสรุปสมการพาราโบลาออกมาได้ดังนี้

โจทย์พาราโบลา

เรียงจากง่ายไปยากนะครับ ลองทำกันดูนะ

EX1: จงหาสมการของพาราโบลาที่มีจุดโฟกัส (0,3) และจุดยอด (0,0)

วิธีทำ จากโจทย์ที่กำหนดให้ เราสามารถวาดกราฟพาราโบลาได้ดังนี้

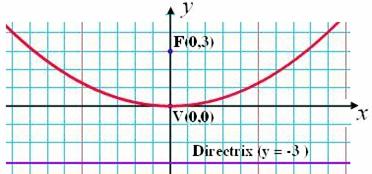
จากรูปเป็นพาราโบลาหงาย มีจุดยอดคือ (0,0) จุดโฟกัสคือ (0,3) และได้ค่า c=3

สมการพาราโบลาของกราฟนี้คือ x²=4cy แทนค่า c=3 ในสมการจะได้

x²=(4)(3)y

x²=12y

#Answer

EX2: จงหาสมการของพาราโบลาที่มีจุดยอด (0,0) มีแกน x เป็นแกนพาราโบลา ความยาวของลาตัสเลกตัมเท่ากับ 12 หน่วย

วิธีทำ จากโจทย์ที่กำหนดให้ เราสามารถหาค่า c ได้จากสูตร

ลาตัสเลกตัม = |4c|

12 = |4c|

c = +- 3

เราสามารถวาดกราฟพาราโบลาได้ดังนี้

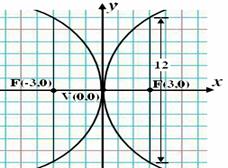จากรูปเราจะได้กราฟพาราโบลาสองอัน เป็นเปิดขวาและเปิดซ้ายอย่างละอัน

สมการพาราโบลารูปขวาคือ

y²=(4)|3|x

y²= 12x

สมการพาราโบลารูปซ้ายคือ

y²= -(4)|3|x

y²= -12x

#Answer

EX3: จงหาสมการของพาราโบลาที่มีจุดยอด (2,3) และจุดโฟกัส (6,3)

วิธีทำ จากโจทย์กำหนดให้ และสมบัติของพาราโบลา เขียนรูปได้ คือ

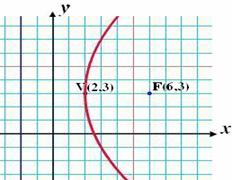จากรูปเป็นพาราโบลาเปิดทางขวา และ และ F (h + c , k) = (6 , 3)

นั่นคือ h + c = 6 แทนค่า h = 2, c = 4 จะได้

(y-k)² = 4*|c|(x-h)

(y-3)² = 4*|4|(x-2)

y²-6y+9=16x-32 —- ใช้สูตรกำลังสองสมบูรณ์

y²-16x-6y+41=0

ดังนั้นสมการพาราโบลาคือ y²-16x-6y+41=0

#Answer

ข้ามไปยังเนื้อหา:

สำหรับ คนที่สนใจอยากเรียนคณิตศาสตร์เรื่องภาคตัดกรวย และบทอื่นๆ แต่ไม่อยากอ่านเอง อยากดูในรูปแบบคลิปวีดีโอมากกว่า พี่มีของดีมาแนะนำครับ คลิปวีดีโอสอนเรื่องความน่าจะเป็นครบทุกหัวข้อ และบทเรียนอื่นๆในระดับชั้นมัธยมอีกครบถ้วน สอนอย่างละเอียดตั้งแต่เริ่มต้น พร้อมด้วยโจทย์เรื่องภาคตัดกรวยเรียงจากง่ายไปยาก ลองอ่านข้อความด้านล่างนี้ดูนะครับ