เป็นเนื้อหาต่อของเรื่องภาคตัดกรวยนะครับ ต่อจากตอนที่แล้วที่พี่ติวฟรีเขียนเรื่องภาคตัดกรวยเบื้องต้นไป วันนี้มาต่อกันด้วยเนื้อหาเรื่องสมการวงกลม จากเรื่องภาคตัดกรวย วิชา คณิตศาสตร์ ม.4 ครับ
สมการวงกลม
วงกลม คือเซตของจุดทุกจุดซึ่งห่างจากจุดคงที่จุดหนึ่งเป็นระยะทางคงตัว จุดคงที่ เรียกว่า จุดศูนย์กลาง ส่วนระยะคงที่เรียกว่า รัศมี
นิยามของสมการวงกลมคือ
วงกลม (circle) คือเซตของจุดทั้งหมดในระนาบที่ห่างจากจุดๆหนึ่งตรึงอยู่กับที่เป็นระยะทางคงตัว จุดที่ตรึงอยู่กับที่นี้เรียกว่า จุดศูนย์กลาง (center) ของวงกลม และระยะทางคงตัวดังกล่าวเรียกว่า รัศมี (radius) ของวงกลม
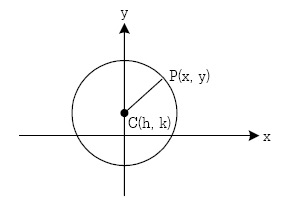
รูปที่ 1: สมการวงกลม
จุด C(h,k) เป็นจุดคงที่ เรียกว่า จุดศูนย์กลาง
|CP| = ระยะทางคงที่ เรียกว่ารัศมี
รูปแบบของสมการวงกลม

รูปที่ 2: รูปแบบของสมการวงกลม
ข้อสังเกตุ
- ถ้า D2 + E2 – 4F = 0 กราฟที่ได้จะเป็นจุดวงกลม
- ถ้า D2 + E2 – 4F > 0 กราฟที่ได้จึงเป็นวงกลม
- ถ้า D2 + E2 – 4F < 0 จะไม่เกิดกราฟในระบบจำนวนจริง
ข้อสำคัญ
ในเรื่องวงกลม ถ้าต้องการหาสมการวงกลม จะต้องทราบ
- จุดศูนย์กลาง
- รัศมี
การหาจุดศูนย์กลางของวงกลม
การหาจุดศูนย์กลางของวงกลม จะหาได้ด้วยวิธีดังต่อไปนี้
- โจทย์กำหนดมาให้โดยตรง เช่นให้จุดศูนย์กลางคือ C(h,k)
- โจทย์กำหนดมาให้ทางอ้อม เช่นจุดที่เส้นตรงตัดกัน
- โจทย์หำหนดมาให้ โดยมีความสัมพันธ์กับกราฟอื่นๆ
การหาความยาวรัศมี
การหาความยาวรัศมี จะหาได้ด้วยวิธีดังต่อไปนี้
- โจทย์กำหนดมาให้โดยตรง (2¶r)
- โจทย์กำหนดมาให้ทางอ้อม เช่นความยาวระหว่างจุดสองจุด หาได้จากสูตร

- โจทย์กำหนดจุดศูนย์กลาง (h, k) และเส้นสัมผัส Ax + By + C = 0 เราจะหาทั้งเส้นผ่านศูนย์กลางและรัศมีได้จากสูตรต่อไปนี้

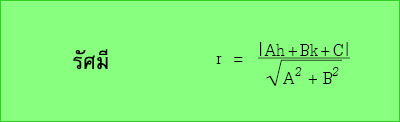
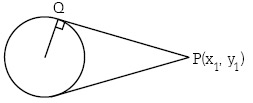
ความยาวของเส้นสัมผัส
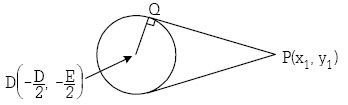
ให้ |PQ| เป็นความยาวของเส้นสัมผัสที่ลากจากจุด P มาสัมผัสวงกลมที่จุด Q
1. ถ้าสมการวงกลมคือ x2 + y2 = r2 แล้ว |PQ| =![]() ดังรูป
ดังรูป
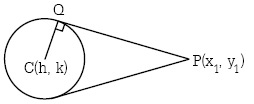
2. ถ้าสมการวงกลมคือ (x-h)2 + (y-k)2 = r2 แล้ว |PQ| = ![]() ดังรูป
ดังรูป
3. ถ้าสมการวงกลมคือ x2 + y2 + Dx + Ey + F = 0 แล้ว |PQ| = ![]() ดังรูป
ดังรูป
ตัวอย่าง
ตัวอย่างที่ 1
จงเขียนกราฟของสมการ (x + 2)2 + (y – 3)2 = 16
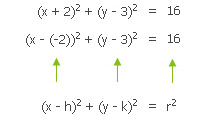
วิธีทำ กราฟของสมการที่กำหนดให้เป็นวงกลม ในการเขียนกราฟ จะต้องทราบตำแหน่งของจุดศูนย์กลางและความยาวของรัศมีของวงกลม ซึ่งหาได้โดยการเทียบสมการที่กำหนดให้กับรูปแบบมาตรฐานของสมการวงกลม จะพบว่า h = -2, k = 3 และ r – 4 ดังนั้น วงกลมมีจุดศูนย์กลางอยู่ที่ (-2, 3) และรัศมียาว 4 หน่วย การเขียนวงกลมขั้นแรก ลงจุดศูนย์กลางที่จุด (-2, 3) และเนื่องจากรัศมีของวงกลมยาว 4 หน่วย ลงจุดอีก 4 จุดห่างไปจากจุดศูนย์กลางไปทางด้านซ้าย ทางด้านขวา ทางด้านล่าง และทางด้านบน 4 หน่วย แล้ววาดวงกลมผ่านจุด 4 จุดนี้จะได้วงกลมดังแสดงในรูป
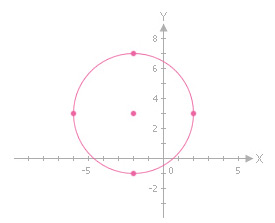
#Answer
ตัวอย่างที่ 2
จงเขียนรูปแบบมาตรฐานของสมการวงกลมที่มีรัศมียาว 3 หน่วย และจุดศูนย์กลาง อยู่ที่ (2, -1)
วิธีทำ จากรูปแบบมาตรฐานของวงกลม (x – h)2 + (y – k)2 = r2
แทน r, h และ k ด้วย 3, 2 และ -1 ตามลำดับ
(x – 2)2 + (y – (-1))2 = 32
(x – 2)2 + (y + 1)2 = 9
รูปแบบมาตรฐานของสมการวงกลมที่มีรัศมียาว r หน่วย และจุดศูนย์กลางอยู่ที่จุดกำเนิด (0, 0) คือ x2 + y2 = r2
วงกลมที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิดและรัศมียาว 1 หน่วย เรียกว่า วงกลมหนึ่งหน่วย (unit circle) และมีสมการเป็น x2 + y2 = 1 ดังแสดงในรูป
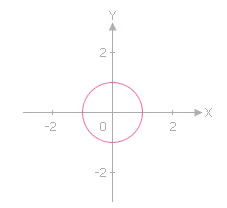
จากสมการของวงกลมในตัวอย่างที่ 2
(x – 2)2 + (y + 1)2 = 9
เมื่อหาผลการยกกำลังสองของ x – 2 และ y + 1 จะได้
x2 – 4x + 4 + y2 + 2y + 1 = 9 หรือ x2 + y2 – 4x + 2y – 4 = 0
ซึ่งเป็นกรณีหนึ่งของสมการ x2 + y2 + ax + by + c = 0 เมื่อ a, b และ c เป็นค่าคงตัว สามารถพิสูจน์ได้ว่าสมการในรูปแบบ x2 + y2 + ax + by + c = 0 มีกราฟเป็นวงกลม หรือจุดหนึ่งจุด หรือไม่มีกราฟ
ตัวอย่างเช่น กราฟของสมการ x2 + y2 = 0 คือจุดหนึ่งจุดคือ จุด (0, 0) สมการ x2 + y2 + 5 = 0 หรือ x2 + y2 = -5 ไม่มีกราฟ เพราะว่าผลบวกของกำลังสองของจำนวนจริงเป็นจำนวนลบไม่ได้ ในกรณีที่สมการ x2 + y2 + ax + by + c = 0 มีกราฟเป็นวงกลม เรียกสมการนี้ว่า รูปแบบทั่วไปของสมการวงกลม
ถ้าสมการของวงกลมอยู่ในรูปแบบทั่วไป สามารถเขียนสมการใหม่ให้อยู่ในรูปแบบมาตรฐานได้โดยใช้วิธีการทำให้เป็นกำลังสองสมบูรณ์
#Answer
ตัวอย่างที่ 3
จงแสดงว่า สมการ x2 + y2 + 2x – 6y + 6 = 0 เป็นสมการของวงกลม แล้วหาจุดศูนย์กลางและความยาวของรัศมีของวงกลม พร้อมทั้งเขียนกราฟ
วิธีทำ ขั้นแรก เขียนสมการที่กำหนดให้ในรูปแบบมาตรฐานของสมการวงกลม โดยจัดกลุ่มของพจน์ที่มี ตัวแปร x และตัวแปร y แล้วทำให้เป็นกำลังสองสมบูรณ์ กล่าวคือ ทำให้ x2 + 2x เป็นกำลังสองสมบูรณ์โดยการบวกด้วย (![]() • 2)2 = 1 และทำให้
• 2)2 = 1 และทำให้
y2 – 6y เป็นกำลังสองสมบูรณ์โดยการบวกด้วย (![]() (-6))2 = 9
(-6))2 = 9
(x2 + 2x) + (y2 – 6y) = -6
(x2 + 2x + 1) + (y2 – 6y + 9) = -6 + 1 + 9
(x + 1)2 + (y – 3)2 = 4
เปรียบเทียบสมการนี้กับรูปแบบมาตรฐานของสมการวงกลมจะได้ว่า h = -1, k = 3 และ r = 2 ดังนั้น สมการที่กำหนดให้เป็นสมการของวงกลมที่มี (-1, 3) เป็นจุดศูนย์กลาง และรัศมียาว 2 หน่วย กราฟเป็นวงกลมแสดงในรูป
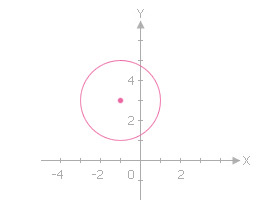
#Answer
ตัวอย่างที่ 4
จงหาสมการเส้นสัมผัสวงกลม x2 + y2 = 13 ที่จุด (2, 3)
วิธีทำ
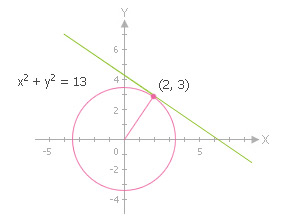
ความชันของรัศมีที่ผ่านจุด (2, 3) คือ ![]()
เส้นสัมผัสของวงกลมที่ผ่านจุด (2, 3) เป็นเส้นตรงที่ตั้งฉากกับรัศมีของวงกลมเส้นที่มีความชัน ![]()
ดังนั้น ความชันของเส้นสัมผัสคือ ![]()
และสมการเส้นตรงที่สัมผัสวงกลมที่จุด (2, 3) คือ
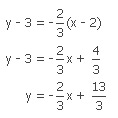
#Answer
ข้ามไปยังเนื้อหา:
สำหรับ คนที่สนใจอยากเรียนคณิตศาสตร์เรื่องภาคตัดกรวย และบทอื่นๆ แต่ไม่อยากอ่านเอง อยากดูในรูปแบบคลิปวีดีโอมากกว่า พี่มีของดีมาแนะนำครับ คลิปวีดีโอสอนเรื่องความน่าจะเป็นครบทุกหัวข้อ และบทเรียนอื่นๆในระดับชั้นมัธยมอีกครบถ้วน สอนอย่างละเอียดตั้งแต่เริ่มต้น พร้อมด้วยโจทย์เรื่องภาคตัดกรวยเรียงจากง่ายไปยาก ลองอ่านข้อความด้านล่างนี้ดูนะครับ


![รวมข้อสอบ O-NET ม.6 พร้อมเฉลย [Download] - Tewfree](https://www.tewfree.com/wp-content/uploads/2020/01/download-ข้อสอบ-o-net-400x209.jpg)









ดีมากๆเรยคร่า
ขอบคุนมากนะคร่า
thank you so much.
Yaranaika?
ดี