ตรรกศาสตร์ เป็นวิชาแขนงหนึ่งที่มีการศึกษาและพัฒนามาตั้งแต่สมัยกรีกโบราณ คำว่า “ตรรกศาสตร์” มาจากภาษาสันสกฤตว่า “ตรฺก” (หมายถึง การตรึกตรอง หรือความคิด) อะริสโตเติล (Aristotle) เป็นผู้หนึ่งที่ได้เขียนตำราทางตรรกศาสตร์ที่เป็นระบบขึ้นเป็นครั้งแรก ซึ่งมีผลต่อความคิดทางปรัชญา ทางวิทยาศาสตร์ และทางศาสนาเป็นอย่างมาก สิ่งที่เราจะได้เรียนกันในระดับชั้น ม.4 นั้นถือว่าเป็นพื้นฐานของวิชาตรรกศาสตร์ เราจึงเรียกมันว่าบทเรียน ตรรกศาสตร์เบื้องต้นนั่นเอง

ตรรกศาสตร์เบื้องต้น

ตรรกศาสตร์ หมายถึง

   ตรรกศาสตร์ เป็นวิชาที่ว่าด้วยกฎเกณฑ์และเหตุผล การได้มาของผลภายใต้กฎเกณฑ์ที่กำหนดถือเป็นสาระสำคัญ  ข้อความหรือการให้เหตุผลในชีวิตประจำวันสามารถสร้างเป็นรูปแบบที่ชัดเจนจน ใช้ประโยชน์ในการสรุปความ  ความสมเหตุสมผลเป็นที่ยอมรับกันอย่างกว้างขวาง ตรรกศาสตร์เป็นแม่บทของคณิตศาสตร์แขนงต่าง ๆ และการประยุกต์

ประพจน์ (Propositions/Statement)

สิ่งแรกที่ต้องรู้จักในเรื่องตรรกศาสตร์คือ ประพจน์ ข้อความหรือประโยคที่มีค่าความจริง(T)หรือเท็จ(F) อย่างใดอย่างหนึ่ง ส่วนข้อความรูป คำสั่ง คำขอร้อง คำอุทาน คำปฏิเสธ ซึ่งไม่อยู่ในรูปของประโยคบอกเล่า จะเป็นข้อความที่ไม่เป็นประพจน์ สำหรับข้อความบอกเล่าแต่มีตัวแปรอยู่ด้วย ไม่สามารถบอกว่าเป็นจริงหรือเท็จจะไม่เป็นประพจน์ เรียกว่าประโยคเปิด

  ประโยคที่มีค่าความจริงไม่แน่นอน  หรือไม่อาจระบุได้ว่ามีค่าความจริงเป็นจริงหรือเป็นเท็จได้ ไม่เป็นประพจน์

การเชื่อมประพจน์

โดยปกติเมื่อกล่าวถึงข้อความหรือประโยคนั้นมักจะมีกริยามากกว่าหนึ่งตัว แสดงว่าได้นำประโยคมาเชื่อมกัน มากกว่าหนึ่งประโยค ดังนั้นถ้านำประพจน์มาเชื่อมกัน ก็จะได้ประพจน์ใหม่ ซึ่งสามารถบอกได้ว่าเป็นจริงหรือเป็นเท็จ ตัวเชื่อมประพจน์มีอยู่ 5 ตัว และตัวเชื่อมที่ใช้กันมากในตรรกศาสตร์คือ และ หรือ ถ้า…แล้ว ก็ต่อเมื่อ  ไม่

1. ตัวเชื่อมประพจน์ “และ”
   การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “และ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∧ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงเป็นจริง (T) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นเท็จ (F)
2. ตัวเชื่อมประพจน์ “หรือ”
   การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “หรือ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∨q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงเป็นเท็จ (F) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นจริง (T)
3. ตัวเชื่อมประพจน์ “ถ้า…แล้ว”
   การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ถ้า…แล้ว” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p → q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p เป็นจริง (T) และ q เป็นเท็จ (F) นอกนั้นมีค่าความจริงเป็นจริง (T)
4. ตัวเชื่อมประพจน์ “ก็ต่อเมื่อ”
   การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ก็ต่อเมื่อ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ⇔ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงตรงกัน และจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงตรงข้ามกัน
5. นิเสธของประพจน์ “ไม่”
   นิเสธของประพจน์ใดๆ คือ ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์นั้นๆ และสามารถเขียนแทนนิเสธของ p ได้ด้วย ~p

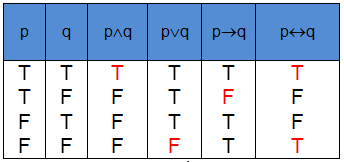
ตารางค่าความจริง

ตารางแสดงค่าความจริงของประพจน์ที่มีตัวเชื่อม พบเห็นบ่อยมากในเรื่องตรรกศาสตร์

ประพจน์ที่สมมูลกัน

ประพจน์ 2 ประพจน์จะสมมูลกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงเหมือนกัน ทุกกรณีของค่าความจริงของประพจน์ย่อย

การทดสอบว่าประพจน์ 2 ประพจน์ สมมูลกัน ทำได้ 2 วิธีคือ

1. สร้างตารางแจกแจงค่าความจริง ค่าความจริงต้องตรงกันทุกกรณี
2. โดยการใช้หลักความจริงและประพจน์ที่สมมูลกันแบบง่ยๆที่ควรจำ เพื่อแปลงรูปประพจน์ไปเป็นแบบเดียวกัน

ตัวอย่างประพจน์ที่สมมูลกันที่ควรทราบ มีดังนี้

p ∧ q     สมมูลกับ    q ∧ p

p ∨ q     สมมูลกับ    q ∨ p

(p ∧ q) ∧ r  สมมูลกับ    p ∧ (q ∧ r)

(p ∨ q) ∨ r  สมมูลกับ    p ∨ (q ∨ r)

p ∧ (q ∨ r)    สมมูลกับ    (p ∧ q) ∨ ( p ∧ r)

p ∨ (q ∧ r)   สมมูลกับ    (p ∨ q) ∧ ( p ∨ r)

p → q   สมมูลกับ    ~p ∨ q

p → q   สมมูลกับ    ~q → ~p

p ⇔ q   สมมูลกับ    (p → q) ∧ (q → p)

ประพจน์ที่เป็นนิเสธกัน

ประพจน์ 2 ประพจน์เป็นนิเสธกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงตรงข้ามกันทุกกรณีของค่าความจริงของประพจน์ย่อย

ตัวอย่างประพจน์ที่เป็นนิเสธกันที่ควรทราบ มีดังนี้

~(p ∧ q)   สมมูลกับ    ~p ∨ ~q

~(p ∨ q)   สมมูลกับ    ~p ∧ ~q

~(p → q)   สมมูลกับ    p ∧ ~q

~(p ⇔ q)    สมมูลกับ    (p ⇔ ~q) ∨(q ⇔ ~p)

~(p ⇔ q)    สมมูลกับ    (p ∧ ~q) ∨ ( q ∧~p)

สัจนิรันดร์

สัจจะ แปลว่าจริง ส่วนนิรันดร์ แปลว่าตลอดกาล ประพจน์ที่เป็นสัจนิรันดร์ คือ ประพจน์ที่มีค่าความจริงเป็นจริง ทุกกรณีของประพจน์ย่อย

ประโยคเปิด (Open Sentence)

คือข้อความที่อยู่ในรูปประโยคบอกเล่าหรือปฏิเสธ ที่มีตัวแปรและสื่อแทนค่าของตัวแปรนั้น จะได้ค่าความจริงแน่นอน หรือเป็นประพจน์ นิยมใช้สัญลักษณ์ P(x), P(x , y), Q(x , y) แทนประโยคเปิดที่มีตัวแปรระบุในวงเล็บ

ตัวบ่งปริมาณ (∀,∃)

ตัวบ่งปริมาณ เป็นตัวระบุจำนวนสมาชิกในเอกภพสัมพัทธ์ที่ทำให้ประโยคเปิดกลายเป็นประพจน์ ตัวบ่งปริมาณมี 2 ชนิด คือ

1. ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกทุกตัวในเอกภพสัมพัทธ์”  ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∀” อ่านว่า”สำหรับสมาชิก x ทุกตัว”
2. ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกบางตัวในเอกภพสัมพัทธ์” ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∃” อ่านว่า “สำหรับสมาชิก x บางตัว”

ค่าความจริงของประพจน์ที่มีตัวบ่งปริมาณ

1. ∀x[P(x)] มีค่าความจริงเป็นจริง เมื่อ x ทุกตัวในเอกภพสัมพัทธ์ทำให้ P(x) เป็นจริง
2. ∀x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อมี x อย่างน้อย 1 ตัวที่ทำให้ P(x) เป็นเท็จ
3. ∃x[P(x)] มีค่าความจริงเป็นจริง เมื่อมี x อย่าน้อย 1 ตัวที่ทำให้ P(x) เป็นจริง
4. ∃x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อไม่มี x ใดๆ ในเอกภพสัมพัทธ์ที่ทำให้ P(x) เป็นจริง

นิเสธของประพจน์ที่มีตัวบ่งปริมาณ

      ~∀x[P(x)] สมมูลกับ ∃x[~P(x)]

      ~∃x[P(x)] สมมูลกับ∀x[~P(x)]

      ~∀x[~P(x)] สมมูลกับ∃x[P(x)]

      ~∃x[~P(x)] สมมูลกับ∀x[P(x)]

การอ้างเหตุผล

การอ้างเหตุผล คือ การอ้างว่า “สำหรับเหตุการณ์ P1, P2,…, Pn ชุดหนึ่ง สามารถสรุปผลที่ตามมา C ได้” การอ้างเหตุผลนี้ ได้รับเลือกเป็นตัวแทนของ ข้อสอบในเรื่องตรรกศาสตร์ ให้เป็นข้อสอบเข้ามหาวิทยาลัย อย่าง O-Net และ PAT1 บ่อยๆ จึงเป็นเรื่องที่สำคัญมาก

การอ้างเหตุผลประกอบด้วย 2 ส่วน คือ

1. เหตุ หรือสิ่งที่กำหนดให้
2. ผล หรือสิ่งที่ตามมา

สำหรับการพิจารณาว่า การอ้างเหตุผลนั้นสมเหตุสมผลหรือไม่นั้นพิจารณาได้จากประพจน์ ( P1 ∧ P2 ∧ … Pn) → C ถ้าประพจน์ดังกล่าวมีค่าความจริงเป็นจริงเสมอ (เป็นสัจนิรันดร์) เราสามารถสรุปได้ว่าการอ้างเหตุผลดังกล่าวเป็นการอ้างที่สมเหตุสมผล
ตัวอย่างเช่น

เหตุ     1. p → q
2. p
ผล       q

ข้อสอบตรรกศาสตร์เบื้องต้น

เป็นอย่างไรกันบ้าง จบกันไปแล้วนะครับสำหรับเนื้อหาเรื่อง ตรรกศาสตร์เบื้องต้น ม.4 น้องๆหลายคนอาจจะคิดว่ายาก แต่พอมาตอนนี้ ตรรกศาสตร์ไม่ยากเลยใช่ไหม ซ้อมทำโจทย์ตรรกศาสตร์กันเยอะๆนะจะได้เก่งๆ วันนี้ได้ความรู้เรื่องตรรกศาสตร์กันไปเต็มๆแล้ว คราวหน้าเตรียมพบกับเนื้อหาบทใหม่กันได้ พบกันใหม่ครับ